If you were in school before common core math was introduced in the 2010s, you might be confused when your child brings home a second-grade math problem covered in diagrams, grids, and arrows. Math has changed a bit, but that’s OK. It may not feel like it, but really smart people are constantly working behind the scenes to improve even the simplest equations.
Common core math is designed to give kids a better handle on the kinds of math problems us grown-ups do every day, and as a bonus, it sneaks in the foundations for advanced problem solving they’ll learn later on in school.
Here at Quotacy, we typically talk about life insurance, but this time, we want to give you the tools to help the ones your life insurance protects: your kids. This blog will help walk through the basics of common core math from addition to division, and show you how it translates to the math skills you already use every day.
Sound good? Good.
Addition
Kindergarten addition is probably the first place you’ll see common core diagrams – these guys. The blocks, sticks, and dots, and the number line.
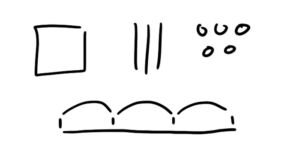
These diagrams are designed to help kids see how big numbers are made out of the smaller numbers they’re already familiar with. We’ll start by explaining the blocks, sticks, and dots.
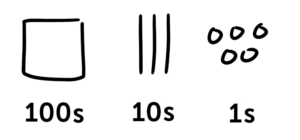
In the common core guidebook, blocks represent hundreds, lines represent tens, and dots represent ones. By grouping them up and shuffling them around, kids can solve difficult equations by doing a few simple math problems instead of one big one. This method of breaking big problems up is one of the core concepts of common core math.
So, for example, let’s take 456 + 167. You start by breaking both numbers down into their base parts – hundreds, tens and ones.
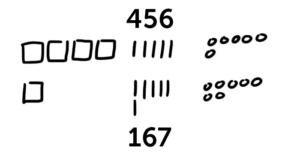
Then, you add based on place. 4+1 is 5, so we have 5 hundreds. 5 plus 6 is 11 tens, or 110, and 6 plus 7 ones is 13. 500 plus 110 is 610, plus 13 is 623.
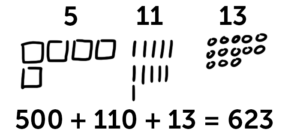
Personally, this is actually how I use math in my day-to-day, like counting bills in my wallet: 5 hundreds, 11 tens, and 13 ones means I have $623.
The number line demonstrates this same idea in a different way. Instead of breaking up both numbers, it shows kids that you can add simple chunks into an existing number to make the math easier.
So for the same problem as before, we start with 456, then you look at the 167 and find easy ways to break it down.
The recommended way to tackle this problem is to pull 100 from the 167, making 556. Then you can add 50 to reach 606, then 10 for 616, then 7 to get 623.
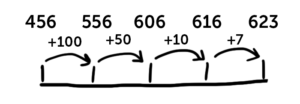
This format helps kids flex their math skills on both addition and subtraction, and gets them to show their work along the way.
One of the main points of frustration for parents here is that teachers often require their students to show their work on a number line for every problem instead of just using it as a tool for kids who need it. I totally get that frustration, but there’s a point.
If you remember when you were at school, you know that teachers hammer skills like this in over and over again to make sure that their students can use them fluently, even if they don’t always need to.
If they ever do get stumped on a future problem and want to sketch out a quick number line to help them think through it, they need to know how it works to get the right answer.
Advanced Addition
The good news is that by grade 2 or 3, kids should have moved past these drawings and gotten into more familiar addition using a method like the one we learned. This is a relief to most parents, but there’s a minor change here too.
Instead of carrying the one all the way up to the top of the number line to sit above your numbers like I was taught, teachers are now encouraging students to put a tens place number on the equation line itself, like this.
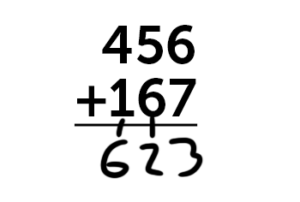
I actually think this is an awesome change, since it lets kids solve problems in a way that feels more like writing numbers out more naturally.
It works really nicely for bigger numbers, too. Take a big equation like 456789 + 167189, for example. Start with 9+9, which is 18, and write it out with the 1 on the equation line. Then keep going, 8+8+1 is 17, 7+1+1 is 9, and so on and so forth.
At this point, addition should look a lot more like what you’re used to, and your kids should already be beginning to dip their toes into subtraction. Thankfully, it’s not too different from what we learned in school.
See what you’d pay for life insurance
Subtraction
The only change in the subtraction process is one designed to help kids avoid one of the most common early mistakes they make – accidentally subtracting a lower number from the higher number. In the common core-taught method for subtraction, you begin the problem by unpacking all the numbers that don’t subtract cleanly before you actually start subtracting.
It’s easier to show you before I explain it. Let’s do 623 – 456.
Ok, I’ll slow it down a bit. First, you check the hundreds to see whether you can subtract cleanly. 6 is greater than 4, so there’s no problem there so far.
Then you check the tens place. 2 is less than 5, so it needs to borrow from the hundreds column, giving you 5 and 12.
Finally, 3 is less than 6, so it has to borrow from the 10s.
We end up with three separate, smaller equations: 5 – 4 = 1, 11 – 5 = 6, and 13 – 6 = 7. 167.
This is a bit of a measure-twice cut-once mentality that can take a while for larger numbers, but it helps kids work on the place-grouping skills they learned about in addition, which will become really important in multiplication and division.
Multiplication
This is where things really start to come together in common core math. Multiplication is where we begin to see how versatile this method of breaking equations down can be, giving your kid glimpses of the more complex math thinking they’ll use in algebra, geometry, and even calculus.
Just like in addition and subtraction, the suggested method for multiplication lets kids multiply big numbers by breaking them up and falling back on their times tables.
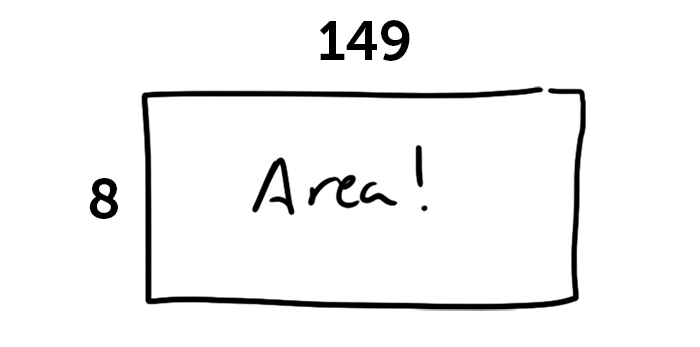
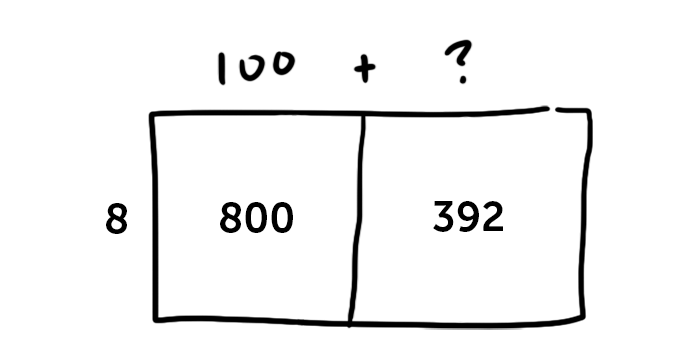
One of the first concepts kids learn is that multiplying two numbers is the best way to find the area of a rectangle – length times width equals area. So let’s say we’re multiplying 8 x 149. We can think about it as trying to find the area of a rectangle that’s 149 feet (or miles, or meters, or inches, you get the idea) on one side and 8 feet long on another.
We also know from addition that numbers can be broken into smaller pieces and worked on individually, and this is still true for multiplication. 149 is a big, scary number, but you can break it up into 100 + 40 + 9, which are easier to work with.
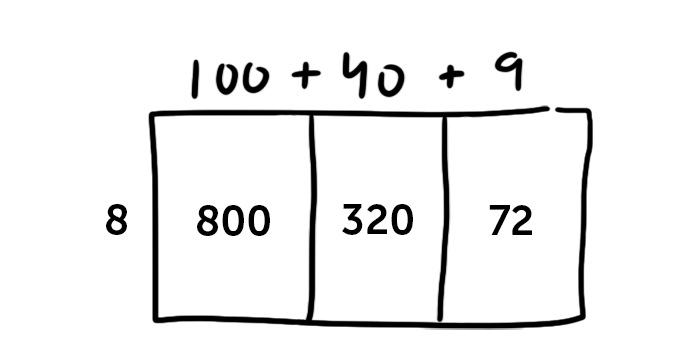
That’s the backbone of common core multiplication. Instead of multiplying 8 by 149, we can make 3 smaller rectangles: 8 x 100, plus 8 x 40, plus 8 x 9.
8 x 1 = 8, so 8 x 100 = 800. 8 x 4 = 32, so 8 x 40 = 320, and 8 x 9 = 72. Some quick addition gets us to 1192.
We can carry this type of method forward into larger numbers as well. For example, 36 x 94. By drawing our rectangle like this, we can see how it works.
A good rule of thumb to know here is that zeroes in a multiplication problem are easy to ignore and add in later. For example, take 90 x 30. Those aren’t on our times tables, but 9 and 3 are.
To solve 90 x 30, you can just remove the zeroes to get 9 x 3, which we know is 27. Then you can add the two zeroes back in to get 2700, which is the correct answer. There’s math that explains exactly how this process works, but kids don’t need to understand the details of it until they get deep into algebra.
Anyway, back to our fourth-grade problem. 30 x 90 is 2700, 30 x 4 is 120, 90 x 6 is 540, 6 x 4 is 24. Some more quick addition gets us to 3384.
By breaking each number up by place and multiplying them one piece at a time, kids can stick within their times tables up to nine, then add on the zeroes from each place at the end. This makes these problems much easier to solve on paper, even after they move past needing the area diagram for reference.
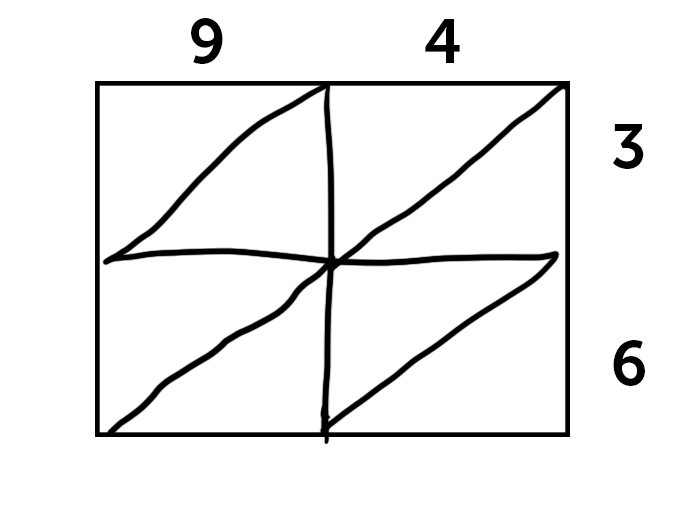
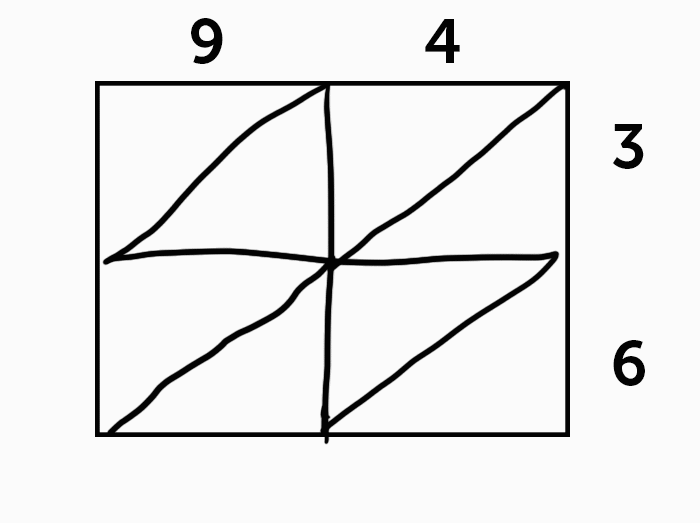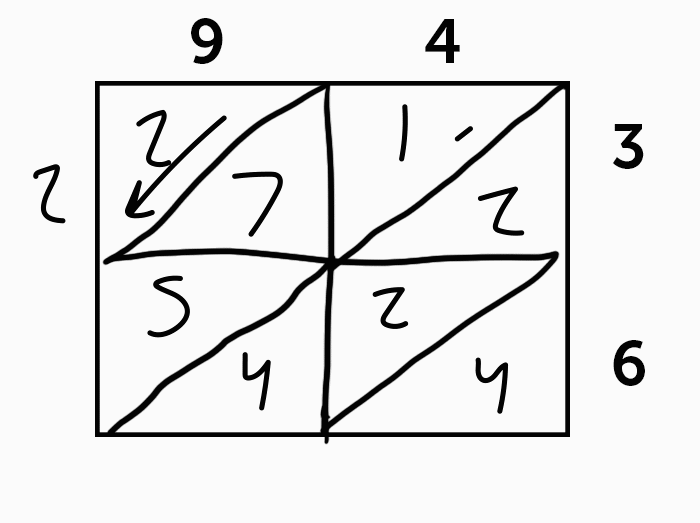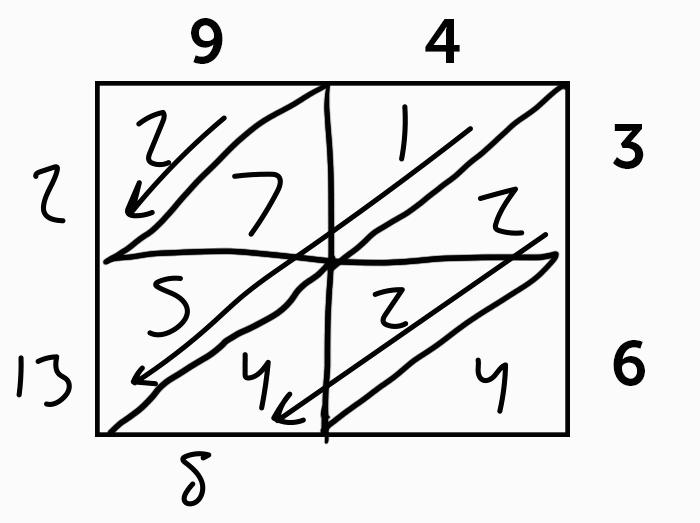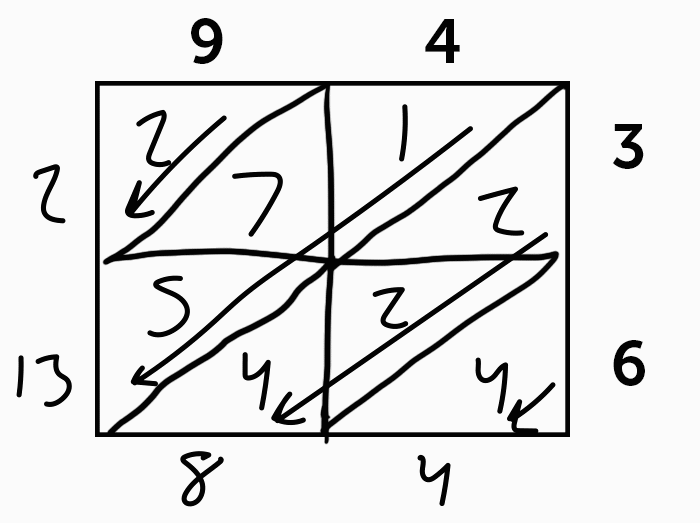
Even though common core math has come into fashion, some teachers have stuck to the slightly older “Lattice” method for multiplication. This is kind of like the common core area method on training wheels – it’s more about memorization than understanding the relationship between length and area.
Basically, you lay out your squares to multiply like before, but add diagonal slashes through them, like this.
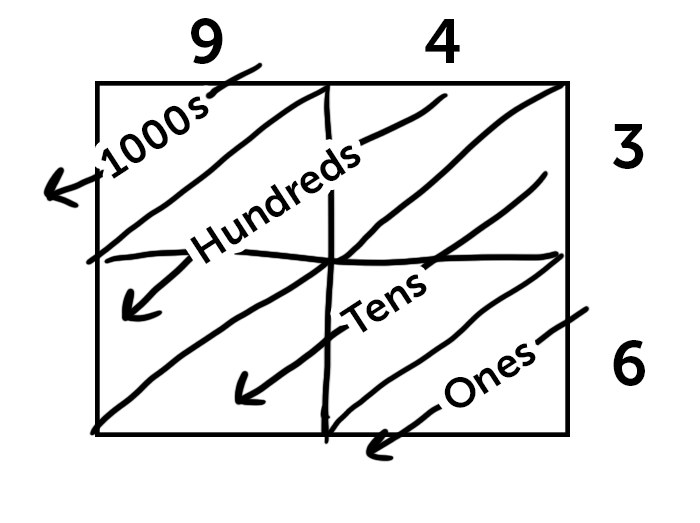
The basic idea of the lattice method is that you multiply each number based on the square they intersect in, then use these diagonal lines to help keep track of the place each result ends up.
Since you’re only ever multiplying under 10, the result of each individual square is always going to be 1 or 2 digits. So, for 94 x 36, starting from the top left, we have 9 x 3 which is 27. 4 x 3 is 12, 9 x 6 is 54, and 4 x 6 is 24.
Then we add based on the diagonal lines for place, giving us 2 thousands, 13 hundreds, 8 tens, and 4 ones. 2000 + 1300 + 80 + 4 = 3384.
I tend to prefer the first method for multiplication, since I personally find it easier to do in my head, and it does a better job at teaching kids the relationship between area and multiplication, which they’ll need later on in school.
However, the lattice method might come more naturally to your child, so if they’re struggling with multiplication using the common core method, it might be a good alternative to help them ace their tests.
Finally, we have division, which flips the multiplication method on its head.
Division
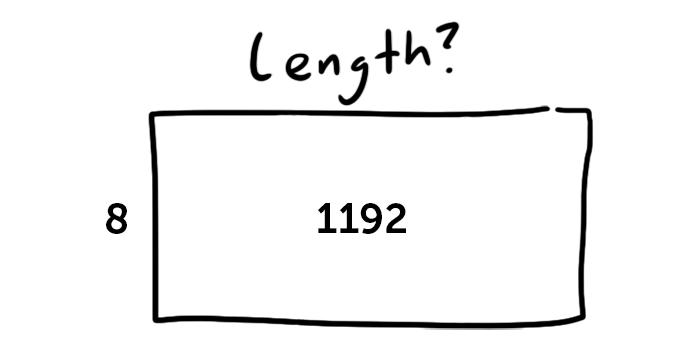
To start us thinking about division in common core, we have to go back to our rectangle. When we divide, instead of knowing the lengths of both sides and trying to find the area, we know the area and one side length. Our goal is to find the length of the other side. Let’s look at this problem: 1192 / 8.
This is the same rectangle we used to learn common core multiplication, so we already know that the answer is 149, but knowing where we’re going will make things a little easier to explain.
In common core math, this problem is also explained by breaking it up into chunks based on place, just like our other problems. To get started, we need to figure out the biggest place number we can multiply 8 by that will still fit inside of our area number.
8000 is way too big, but 800 is smaller than our area. This means we can start with hundreds. 800 fits inside 1192, but 1600 doesn’t, so we know that only 1 hundred fits. Since 800 of our area is accounted for, so we can subtract to get a smaller number to keep working with. 1192 – 800 is 392.
Since units of 800 can’t fit into our area anymore, we can move on to the tens place and use units of 80. 80 fits into 392 4 times, which is 320, and 392 – 320 is 72.
Finally, we end up with 72 / 8. If we remember our times tables, we know that 8 x 9 is 72, which accounts for all the remaining area. This leaves us with 149 as the length of our missing side.
Written out on paper instead of using a diagram, we can see that it actually looks a lot like long division, but it ditches the old method of bringing down numbers in favor of using the place units kids learn in common core.
That’s the basics of the common core division method, and with that, you now you know the backbone of common core math. At its most basic level, common core math is about making all these different math concepts play with one another.
I worked in construction for most of my high school career, and I powered through quite a few math classes before I realized I didn’t want to be a mechanical engineer, so I was surprised to see how versatile these methods are.
You could easily use them for everyday math problems like counting money or figuring out square footage in a room. However, I can see how being taught from a young age to think about numbers in a fluid way like this would have helped me in math classes well into college.
Long story short, common core math might be overly complex at first glance, but it offers your kids a comprehensive way of looking at numbers that will keep being valuable their whole lives.
It can be tough to re-learn math as an adult, but who knows? Maybe your kids’ kids will learn an even better way to do math than common core, and they’ll finally learn how you feel right now.




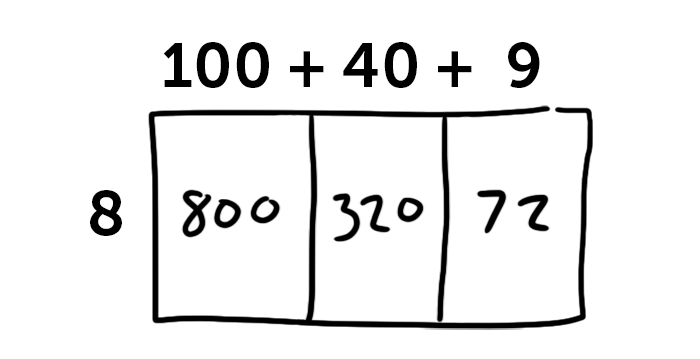
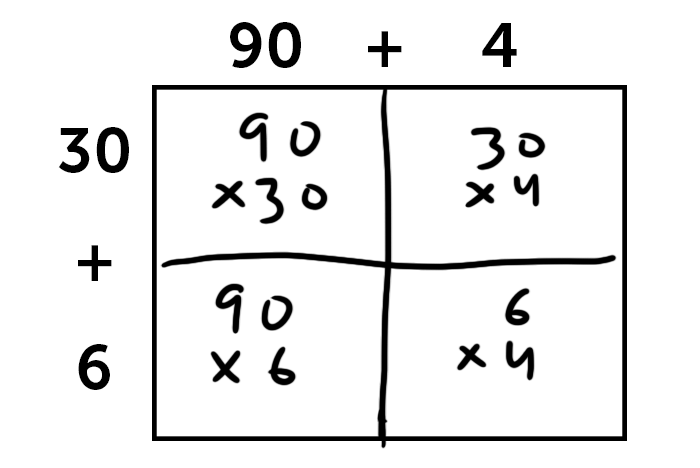

The whole point of getting kids to show their work is to show that even if they find their own way, they understand the concept. Up until I’d say grade 2 we were still given marks for work that was right, even if the answer was wrong, ie. Doing the correct multiplication formula but messing up with your numbers
I always liked math as a student, even graduated in math honors classes, but this new method blows my mind. I always thought math was the one subject that would remain the same…. until 2010… common core was emplemented into my children’s math classes. Now both of my youngest are 100% virtual, due to covid, that’s when I got a hard lesson on this common core crap. To me it’s longer and more confusing. I struggled at 1st with my 4th grader, while my 8th grader, who’s taking pre algebra, is using the same formulas and methods that I myself was taught . I can go along with introducing new methods, but if my child doesn’t show her work using common core, it’s marked wrong, even if the answer is correct. That I don’t agree with at all, they should be allowed to use the formula or method that suits them, as long as they can get the correct answer.
Or just ignore this whole thing and just add and subtract normally. You want kids building common core houses, common core cars, and common core planes? Look all 3 of those up on Google images.
Exactly it’s over complicated crap… my kids have the worst time with it and handle normal math better… but they will fail if they cant draw pictures. Ok. Common core is horrid for kids with dysgraphia also
Exactly Crys! My kids hate the new common core math, they don’t like drawing the shapes. I always taught them that they shouldn’t need to draw to be able to do their work, and this common crap (I came up with that) math is undoing all that. Kids these days don’t even need to do math anymore, they can just tell Siri to do it for them and problem solved! Doing art is not the same as math AND IT NEVER WILL BE